写在前面
- 由于个人水平有限,故部分内容可能会出现错误,还请包涵
TreeMap 的底层数据结构为红黑树,因此要想理解 TreeMap,必须先理解红黑树。本文重点在于 TreeMap 的解析,故对红黑树的内容只作简单介绍
红黑树之删除节点
红黑树时每个节点都带有颜色属性的二叉查找树,其特性有:
- 1.节点是红色或黑色
- 2.根节点是黑色
- 3.每个叶节点(这里的叶节点是指 NULL 节点,在《算法导论》中这个节点叫哨兵节点,除了颜色属性外,其他属性值都为任意。为了和以前的叶子节点做区分,原来的叶子节点还叫叶子节点,这个节点就叫它 NULL 节点)是黑色的
- 4.从每个叶子节点到根节点的所有路径上不能有两个连续的红色节点
- 5.从任一节点到其每个叶子节点的所有路径都包含相同数目的黑色节点
基本思路
红黑树删除节点的基本思路为找到将被删除节点的后继节点,将后继节点的属性赋给将被删除的节点,然后删除后继节点,对节点的删除不会产生颜色碰撞的情况
而后继节点为:
- 1.单个的叶子节点(不是指 NULL 节点)
- 2.只有单子树的节点(即只有左子树或右子树)
若后继节点为红色,则删除的步骤和普通的二叉查找树的删除步骤基本类似,因为对红色节点的删除不会影响整棵红黑树的黑高。若后继节点为黑色,则情况就要复杂的多,但基本思路还是在于如何将黑色节点删除后部分子树黑高减一的情况消除
具体情况
对于一棵普通的二叉查找树,删除节点的情况可分为 3 种:
- 1.叶子节点
- 2.单子树节点
- 3.双子树节点
我们知道对于一棵普通二叉树的情况 3 来说,要删除既有左子树又有右子树的节点,我们首先要找到该节点的直接后继节点,然后用后继节点替换该节点,最后按 1 或 2 中的方法删除后继节点即可。即情况 3 可以转换成情况 1 或 2
同样,对于红黑树来说,删除节点的实际情况也只有两种。对于情况 2,即待删除的节点有单子树,很多组合在红黑树中是不存在的
情况 2 中不存在的情况有(其中 D 表示要删除的节点,DL 和 DR 分别表示左子树和右子树)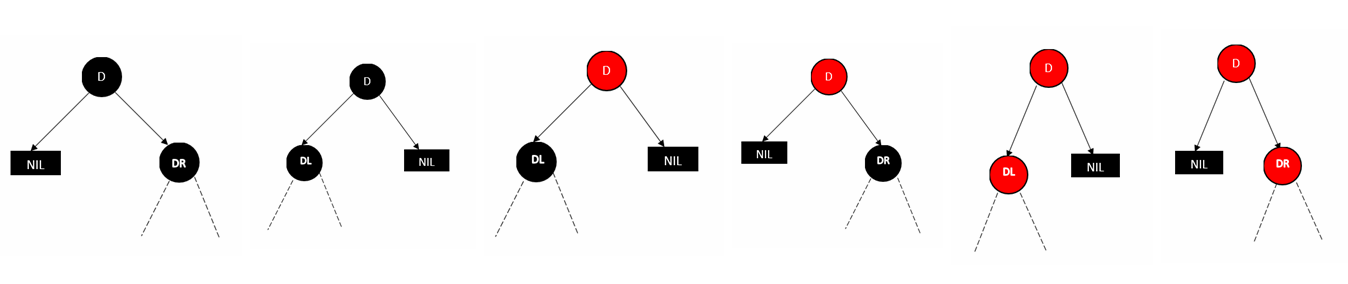
删除红色节点
1.删除红色的叶子节点(D表示待删除的节点,P表示其父亲节点)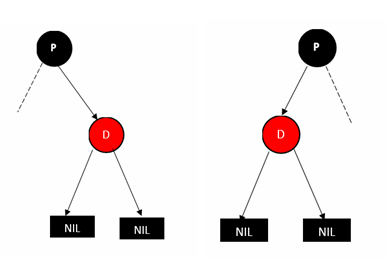
上述两种情况处理方式一致,直接删除 D 节点即可
2.删除的红色节点有单子树
之前已经分析过,红黑树中根本不存在这种情况
删除黑色节点
1.删除的黑色节点有单子树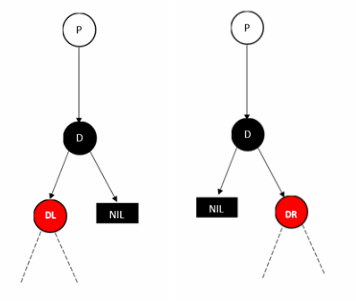
上述两种情况处理方式一致,即用 D 的孩子(左或右)替换 D,并将 D 孩子的颜色改为黑色即可(因为路径上少了一个黑节点,所以将红节点变成黑节点以保持红黑树的性质)
2.删除黑色的叶子节点(此情况最为复杂,因为还要考虑其兄弟节点的颜色情况)
2.1.待删除节点 D 的兄弟节点 S 为红色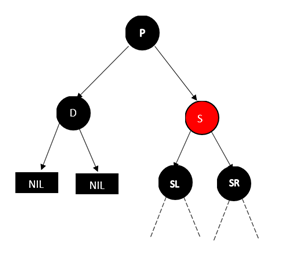
将父节点和兄弟节点的颜色互换,然后对 P 节点进行左旋转,结果如下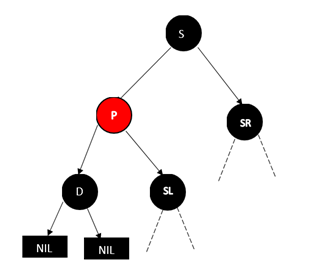
这时,D 的兄弟节点为黑色,转化为下面将要讨论的情况
2.2.兄弟节点为黑色,且远侄子节点为红色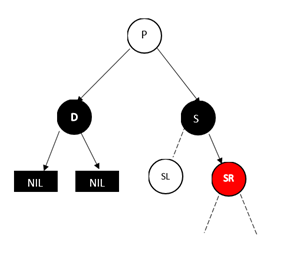
没有上色的节点代表红色黑色均可,注意若 SL 为黑色,则其必为 NULL 节点
此时,若我们直接删除 D 节点,则经过 D 的子节点的路径的黑高将会减一。我们发现 S 节点的孩子中有红色节点,如果可以将该红色节点移动到左侧并将颜色改为黑色,则满足要求。这也是为什么 P 节点的颜色无关,因为调整过程只在 P 整棵子树的内部进行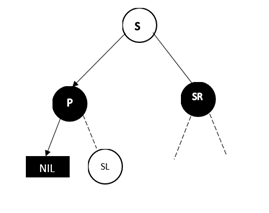
调整过程为,将 P 和 S 的颜色互换,然后对 P 进行左旋转,最后将 SR 改为黑色,删除 D 即可
2.3.兄弟节点为黑色,远侄子节点为黑色,近侄子节点为红色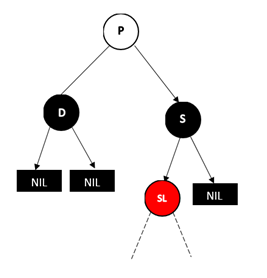
调整过程为对 S 进行右旋转,并将 S 和 SL 的颜色互换,这时情况转为 2.2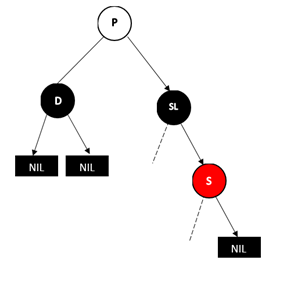
2.4.父节点为红色,兄弟节点和兄弟节点的两个孩子(只能是 NULL 节点)都为黑色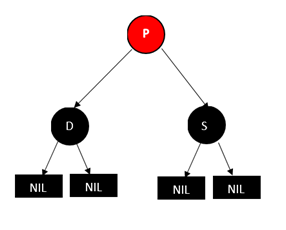
如果删除 D,那经过 P 到 D 的子节点 NULL 的路径上黑高减一,这个时候我们可以把 P 变成黑色,这样删除 D 后经过 D 子节点(NULL 节点)路径上的黑高就和原来一样了。但是这样会导致经过 S 的子节点(NULL 节点)的路径上的黑高加一,所以这个时候可以再将 S 节点变成红色,这样路径上的黑色节点数就和原来一样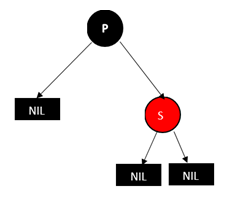
调整过程为,将 P 改为黑色,将 S 改为红色,删除 D 即可
2.5.父节点、兄弟节点和兄弟节点的两个孩子(只能是 NULL 节点)都为黑色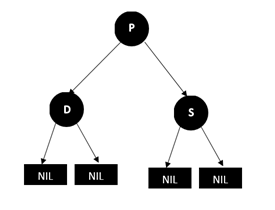
调整过程为,将兄弟节点 S 的颜色改成红色,这样删除 D 后 P 的左右两支的黑节点数就相等了,但是经过 P 的路径上的黑色节点数会少 1,这个时候,我们再以 P 为起始点,继续根据情况进行平衡操作(这句话的意思就是把 P 当成 D(只是不要再删除 P 了),再看是那种情况,再进行对应的调整,这样一直向上,直到新的起始点为根节点
TreeMap
1 | public class TreeMap<K,V> |
TreeMap 是一个有序的 key-value 集合,它是通过红黑树实现的
TreeMap 继承自 AbstractMap,实现了 NavigableMap 接口,意味着它支持一系列的导航方法。比如返回有序的 key 集合
TreeMap 的核心方法有两个,即 put() 方法和 deleteEntry() 方法
deleteEntry
1 | private void deleteEntry(Entry<K,V> p) { |
寻找后继节点的 successor() 方法源码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36static <K,V> TreeMap.Entry<K,V> successor(Entry<K,V> t) {
if (t == null)
return null;
// 若 t 右子树不为空,则寻找右子树中最小的节点为 t 的后继节点
else if (t.right != null) {
Entry<K,V> p = t.right;
while (p.left != null)
p = p.left;
return p;
} else {
// 若右子树为空,则判断 t 是否为其父节点 p 的左子树,若是,则返回 p
// 若不是,则依次迭代往上进行寻找直到找到或寻至根节点
Entry<K,V> p = t.parent;
Entry<K,V> ch = t;
while (p != null && ch == p.right) {
ch = p;
p = p.parent;
}
return p;
}
}
由 successor() 方法的源码我们可以知道,待删除节点的后继节点或为叶子节点,或为有单子树的节点
删除节点后(注意只有删除黑节点才会调用此方法)对红黑树进行调整的 fixAfterDeletion() 方法的源码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117private void fixAfterDeletion(Entry<K,V> x) {
while (x != root && colorOf(x) == BLACK) {
// 只讨论 x 节点为其父节点左孩子的情况,为右孩子的情况与此类似
if (x == leftOf(parentOf(x))) {
Entry<K,V> sib = rightOf(parentOf(x));
// 判断兄弟节点的颜色
// 若为红对应之前的 2.1 情况
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateLeft(parentOf(x));
// 更新 x 节点的兄弟节点
sib = rightOf(parentOf(x));
}
// 兄弟节点的两个孩子颜色均为黑色,对应 2.4/ 2.5 情况
if (colorOf(leftOf(sib)) == BLACK &&
colorOf(rightOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
} else { // 注意此时兄弟节点的两个孩子节点的颜色不可能都为黑
// 远侄子节点颜色为黑,对应 2.3 情况
// 将其转换为 2.2 情况
if (colorOf(rightOf(sib)) == BLACK) {
setColor(leftOf(sib), BLACK);
setColor(sib, RED);
rotateRight(sib);
// 更新 sib
sib = rightOf(parentOf(x));
}
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(rightOf(sib), BLACK);
rotateLeft(parentOf(x));
// x = root 用于终止 while 循环
x = root;
}
} else { // symmetric
Entry<K,V> sib = leftOf(parentOf(x));
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateRight(parentOf(x));
sib = leftOf(parentOf(x));
}
if (colorOf(rightOf(sib)) == BLACK &&
colorOf(leftOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
} else {
if (colorOf(leftOf(sib)) == BLACK) {
setColor(rightOf(sib), BLACK);
setColor(sib, RED);
rotateLeft(sib);
sib = leftOf(parentOf(x));
}
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(leftOf(sib), BLACK);
rotateRight(parentOf(x));
x = root;
}
}
}
setColor(x, BLACK);
}
put
相较于 deleteEntry() 方法而言,put() 方法就要简单许多1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94public V put(K key, V value) {
Entry<K,V> t = root;
// 若根节点为空
if (t == null) {
compare(key, key); // type (and possibly null) check
// new Entry 的默认颜色为黑色
root = new Entry<>(key, value, null);
size = 1;
modCount++;
return null;
}
int cmp;
Entry<K,V> parent;
// split comparator and comparable paths
Comparator<? super K> cpr = comparator;
// 判断用户是否传入了自定义的排序规则
if (cpr != null) {
do {
parent = t;
cmp = cpr.compare(key, t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
else {
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable<? super K> k = (Comparable<? super K>) key;
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
// 若之前的代码没有找到匹配的节点,则创建一个新的节点
Entry<K,V> e = new Entry<>(key, value, parent);
if (cmp < 0)
parent.left = e;
else
parent.right = e;
// 对红黑树进行调整
fixAfterInsertion(e);
size++;
modCount++;
return null;
}
要想理解 fixAfterInsertion() 方法的源码,必须对红黑树插入新节点的规则有所了解
fixAfterInsertion() 方法的源码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84private void fixAfterInsertion(Entry<K,V> x) {
// 新加入的节点颜色均设为红色
x.color = RED;
// 若 x 父节点颜色黑,则插入新的红节点无需对整棵红黑树进行调整
while (x != null && x != root && x.parent.color == RED) {
// 判断 x 的父节点是否为祖节点的左孩子
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
// y 为 x 父节点的兄弟节点
Entry<K,V> y = rightOf(parentOf(parentOf(x)));
// 若 y 为红色节点,则将红色节点的情况往上抛
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
} else { // 若 y 为黑色节点
// 若 x 为父节点的右孩子,则将其转换为左孩子的情况
if (x == rightOf(parentOf(x))) {
x = parentOf(x);
rotateLeft(x);
}
// 对 x 的祖节点进行右旋转
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateRight(parentOf(parentOf(x)));
}
} else { // 若 x 的父节点为祖节点的右孩子
Entry<K,V> y = leftOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
} else {
if (x == leftOf(parentOf(x))) {
x = parentOf(x);
rotateRight(x);
}
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateLeft(parentOf(parentOf(x)));
}
}
}
root.color = BLACK;
}